(String) Prefix Trees (5 Part Series)
1 Implementing Tries in Java
2 Ternary Search Trees
3 Ternary Search Tree: Core Methods (Java Implementation)
4 Prefix Search with Ternary Search Trees (Java Implementation)
5 Java Profiling: comparing BSTs, tries and TSTs
To better understand TST, it’s important to look at some concrete implementations – in particular, I chose to use Java in this series.
 mlarocca / AlgorithmsAndDataStructuresInAction
mlarocca / AlgorithmsAndDataStructuresInAction
Advanced Data Structures Implementation
With recursive structures, like trees and lists, I usually define a class for the container, what will be shared with the clients and implement the public interface of the data structure, and a private class for the list/tree nodes.
public class Tst implements StringsTree {
private TstNode root;
public Tst() {
root = null;
}
public Optional<String> search(String element) {
return root == null || root.search(element) == null ? null : element;
}
...
}
Enter fullscreen mode Exit fullscreen mode
The Tst class is just a wrapper for the root of the tree, and all methods are just forwarded to their equivalents for the single nodes.
Of course, in Java you might also want to define an interface that sets in stone the behavior of the container, if you have another concrete class that can interchangeably perform the same operations (in this case we do, because we can implement a Trie class that has the exact same behavior), or in general if you want to decouple the abstract API from the concrete implementation.
The TstNode class is much more interesting than the tree wrapper, because it contains all the logic.
private class TstNode {
private Character character;
private boolean storesKey;
private TstNode left;
private TstNode middle;
private TstNode right;
public TstNode(String key) {
...
}
Enter fullscreen mode Exit fullscreen mode
It needs to have fields for the three children of a node, and for the character that each node holds.
I t also needs a way to mark nodes that stores a key: in this version of trie/tst, the containers are just sets, holding the strings stored in them, so I used a boolean flag; however, we can easily implement these trees as dictionaries (which will thenn associate a value to each key stored) by replacing the storesKey flag with a generic field for a value, for instance:
private class TstNode<T> {
private Character character;
private T value = null;
private TstNode left = null;
private TstNode middle = null;
private TstNode right = null;
public TstNode(String key, T value) {
if (key.isEmpty() || value == null) {
throw new IllegalArgumentException();
}
character = key.charAt(0);
if (key.length() > 1) {
// Stores the rest of the key in a midlle-link chain
middle = new TstNode(key.substring(1), value);
} else {
this.value = value;
}
}
Enter fullscreen mode Exit fullscreen mode
You can also see the implementation of the constructor for the dictionary version above. Obviously value could be any type inheriting from Object.
Constructing a new node to store a key-value pair is easy: we need to create a middle-link chain (which resembles a linked list, at this point!), so we take the first character in the string, store it in the currently-being-created node, and then (unless is was also the last character) create a sub-tree (or better, a sub-chain of nodes, linked through middle-links), that will be stored as the middle-child of current node.
Notice that value will be stored only in the very last node of the chain.
Adding a New Key-Value Pair
Once we have created our empty TST, we need a method to fill it with key/value pairs. This is probably the one method with which we need to be more careful when we write the TST wrapper, because we can deal with an empty root, and in that case we also assign it.
public boolean Tst<T>::add(String element, T value) {
if (root == null) {
root = new TstNode<T>(element, value);
return true;
} else {
return root.add(element) != null;
}
}
Enter fullscreen mode Exit fullscreen mode
The core of the algorithm, however, still lies in the TstNode class.
In the listings above and below I omitted some of the checks on the arguments just for the sake of space: we want to make sure that the key is not null and not empty, and that the value is not null. We can perform those checks once per client call in Tst::add.
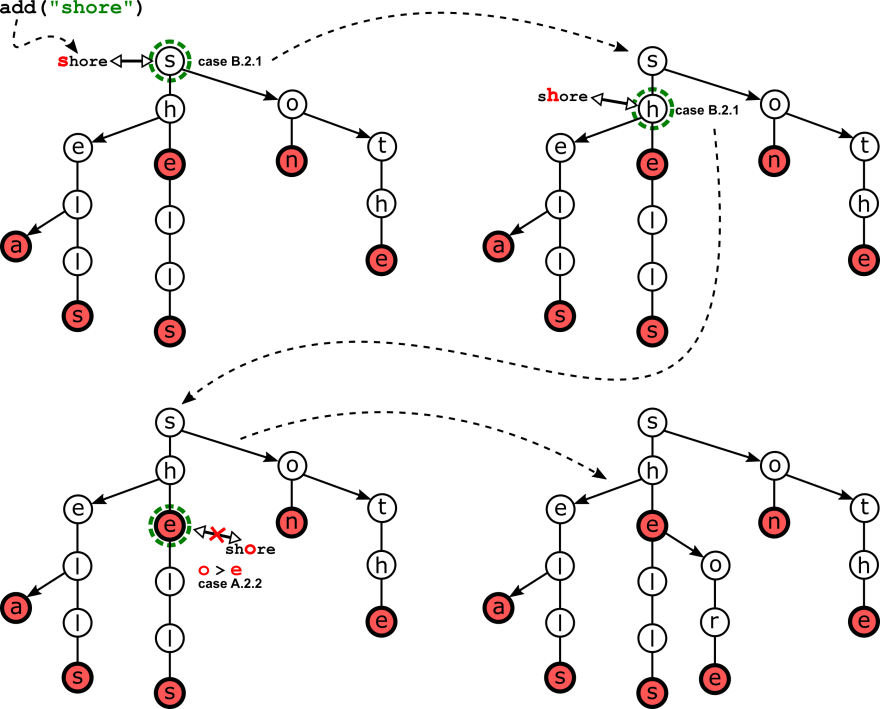
The figure below shows the results of adding words in the tongue-twister "she sells sea shells on the sea shore" to an empty TST. All words are added in the order they appear in the sentence, but we don’t add duplicates ("sea" appears twice ).
Since we start with an empty tree (i.e. Tst::root is null), for the first word, "she", the method just creates a middle-link chain, a list of nodes holding those three characters. As we progress, more and more branches are created, each at the end if the common prefix of an existing word and the newly inserted one.
Let’s pause before adding the last word in the sentence, "shore", and review how the add methods work: then we can use this word to detail a step-by-step example.
The first and most important thing that the method needs to check is (assuming key is not empty) how the first character in the key compares to the character stored in the current node.
- (A) If it’s a mismatch, we need to traverse the left (A.1) or right (A.2) branch respectively (depending on if it’s smaller or larger); if the branch we need to traverse doesn’t exist, then we can just create a new
TstNode-chain that will store the rest of our key, connect it to the current node, and we are done. - (B) If we have a match, then the situation is more interesting. First, are we done with the input key, i.e. is this its last character?
- (B.1) If so, this is the node where we’ll store
value: to distinguish updates to an existing key, we check if a value was already stored in this node. - (B.2) Otherwise, if there are more characters in
keyafter the current one, then the situation can be handled like the ones for left/right branches, with one difference: since we have a match, we have to move to the next character in the input key.
- (B.1) If so, this is the node where we’ll store
private TstNode<T> TstNode<T>::add(String key, T value) {
Character c = key.charAt(0);
if (character.equals(c)) { // case B
if (key.length() == 1) { // case B.1
boolean updated = this.storesKey();
this.value = value;
// We return a non-null node only for insertion, and null for update
return updated ? null : this;
} else if (this.middle != null) { // case B.2.1
return middle.add(key.substring(1));
} else { // case B.2.2
this.middle = new TstNode<T>(key.substring(1));
// We need to find the last node in the chain to return it
return middle.search(key.substring(1));
}
} else if (c.compareTo(character) < 0) { // case A.1
if (this.left != null) { // case A.1.1
return left.add(key, value);
} else { // case A.1.2
left = new TstNode<T>(key, value);
return left.search(key);
}
} else { // case A.2
if (this.right != null) { // case A.2.1
return right.add(key, value);
} else { // case A.2.2
right = new TstNode<T>(key, value);
return right.search(key);
}
}
}
private boolean TstNode<T>::storesKey() {
return this.value != null;
}
Enter fullscreen mode Exit fullscreen mode
Above we also declare the storesKey method, that will be useful to abstract checking if a node is marked as “key node”, regardless of the implementation.
As promised, here it is an example of the method in action, with a call to add("shore") illustrating a few of the cases that are highlighted in the code.
TST Lookup
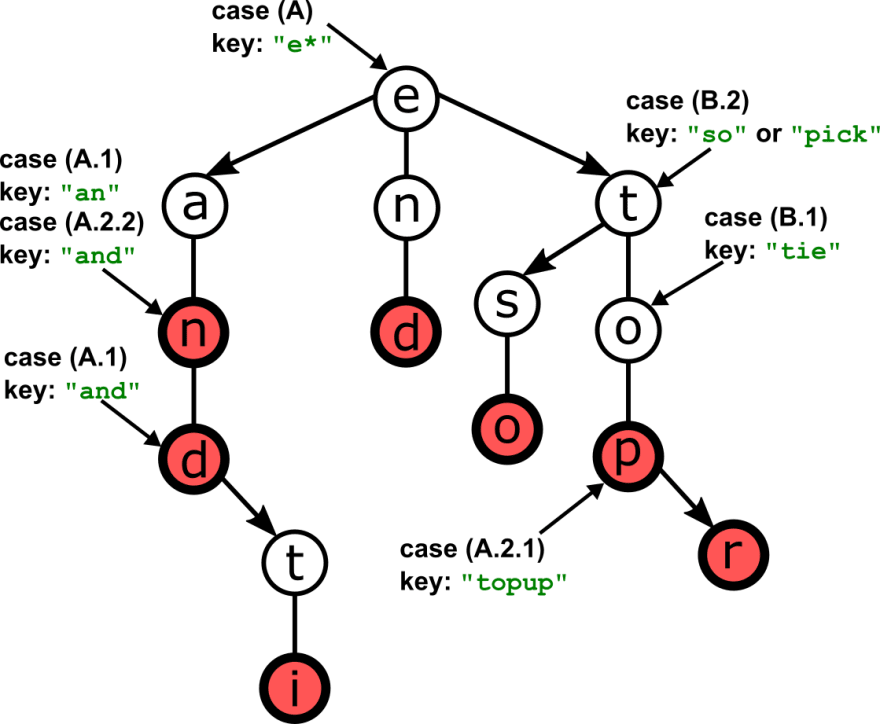
As we have already seen, search works similarly to binary search trees: for each character c in our search string, we first need to find out if, in current sub-tree, there is a node that contains c and is reachable only through left/right links (we can only follow middle-links after a match!).
So, without losing generality, we can restrict to the case where we search for the first character in the string starting from the tree’s root. Both strings and TSTs are recursive structures: each node in a TST is the root of a subtree, and a TST is either an empty tree (base case) or a node with left, middle and right – possibly empty – sub-trees).
To perform search, we can follow these steps:
- We compare root’s character to the first character in the string;
- Case (A) They match: that’s great, we found our string char. Now check: was this the last character in the string?
- Case (A.1): Yes, it was the last one. Now we check if there is a value stored in the current node. If so we have found our search string, otherwise it’s not in the tree.
- Case (A.2) Otherwise, we move to the next character in the string and…
- Case (A.2.1)…if there is no middle link for this node (i.e. it’s a leaf), then the string is not in the tree.
- Case (A.2.2)…if the middle link is not null, we follow the link and repeat the steps from 1.
- Case (B) There is no match between our search string’s char and our node’s char. If the former is smaller we go left, if it’s larger we go right.
- Case (B.1) If the link we were supposed to follow is null (no left or right child respectively), then our search string is not in the tree.
- Case (B.2) Otherwise, we just traverse the link and repeat from step 1.
The following figure illustrates some of the cases above on an example trie.
Let’s put this into some Java code:
public TstNode<T> search(String key) {
if (key.isEmpty()) {
return null;
}
Character c = key.charAt(0);
if (c.equals(this.character)) { // case A
if (key.length() == 1) { // case A.1
return this;
} else { //case A.2
return this.middle == null
? null // case A.2.1
: this.middle.search(key.substring(1)); // case A.2.2
}
} else if (c.compareTo(this.character) < 0) { // case B.1
return left == null ? null : left.search(key);
} else { // case B.2
return right == null ? null : right.search(key);
}
}
Enter fullscreen mode Exit fullscreen mode
Now, in practice we would like to avoid all those calls to String::substring, because each of them needs to create a new string, and traversing a large tree this gets really expensive.
The good news is that we can easily find a workaround by just passing around the index of the next character to check. It’s not as elegant, and we’ll need to define a private method to keep the public API clean, but the efficiency boost we get is really worth it.
public T Tst<T>::search(String key) {
TstNode node = search(key, 0);
return node != null && node.storesKey() ? node.value : null;
}
private TstNode<T> search(String key, int index) {
if (index >= key.length()) {
return null;
}
Character c = key.charAt(index);
...
}
Enter fullscreen mode Exit fullscreen mode
Delete
The next base operation we would like to perform on a container is… removing elements.
Surprise surprise, this method follows the same structure as the other two: comparing the first character in the key passed, and then choosing the right branch to traverse depending on the result.
If it wasn’t for a caveat, we could have implemented remove almost by cutting and pasting search.
Where is the catch? Well, if you think about it, what’s always the catch, in Java but also in all other programming languages, when you delete something from a collection?
If we are not careful, of course, we won’t free the space previously used.
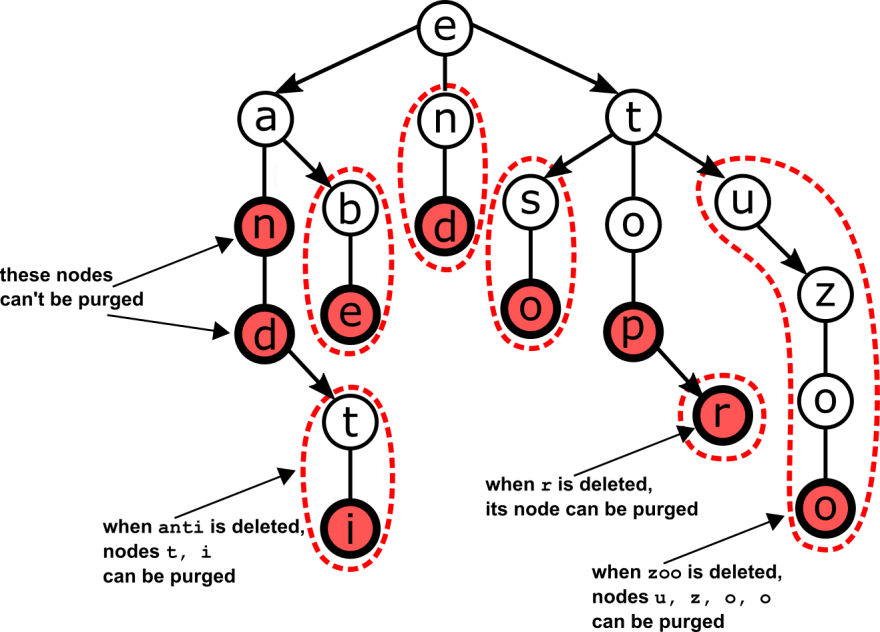
You can see from the figure below that, for such trees like TSTs, there are cases where we can’t free any space, because we are deleting a key stored in an internal node. But whenever we delete a key from a leaf, we can delete that node, and all its ancestors that both don’t store any key/value, and have no siblings.
private boolean remove(String key, AtomicBoolean purge) {
Character c = key.charAt(0);
if (c.equals(this.character)) {
if (key.length() == 1) {
if (this.storesKey()) {
value = null;
// If this node stores a key, and it's a leaf,
// then the path to this node can be purged.
purge.set(this.isLeaf());
return true;
} else {
return false;
}
} else {
boolean deleted = this.middle == null
? false
: this.middle.remove(key.substring(1), purge);
if (deleted && purge.get()) {
this.middle = null;
purge.set(!this.storesKey && this.isLeaf());
}
return deleted;
}
} else if (c.compareTo(this.character) < 0) {
boolean deleted = left == null ? false : left.remove(key, purge);
if (deleted && purge.get()) {
this.left = null;
purge.set(!this.storesKey() && this.isLeaf());
}
return deleted;
} else {
boolean deleted = right == null ? false : right.remove(key, purge);
if (deleted && purge.get()) {
this.right = null;
purge.set(!this.storesKey() && this.isLeaf());
}
return deleted;
}
}
Enter fullscreen mode Exit fullscreen mode
The remove method is still conceptually easier than binary search tree’s or, even worse, treaps, because we don’t have to perform any rotation nor replace the deleted node with the minimum or maximum of its subtree.
We simply check, while backtracking, that we can remove the link we had traversed and, if so, if current node becomes itself eligible for being purged; the condition to meet is simple: a node can be purged when it’s a leaf and it doesn’t store a key.
Notice that, the way this method is implemented here, it will never purge the root of the tree. This won’t cause problems, but if you’d like to go the extra mile, you’ll need to check, in
Tst::remove, if after the call toroot.removereturns theAtomicBooleanflagpurgeis set totrue: if that’s the case, you can setroot = null.
Performing this purging is not, however, mandatory: if we know that the rate between add and remove operations is highly skewed towards insertions (and possibly deleted keys get periodically re-inserted), or even better if we have a high ratio of reads-to-writes, we can decide it’s not worth to get into the trouble of purging nodes.
Why would you not free-up deleted nodes? First and foremost, it allows you to write a shorter, cleaner and more efficient method: check out the difference in the following snippet, where we called this variant removeNGC as in “no garbage collection”.
private boolean removeNGC(String key) {
Character c = key.charAt(0);
if (c.equals(this.character)) {
if (key.length() == 1) {
if (this.storesKey()) {
value = null;
return true;
} else {
return false;
}
} else {
return this.middle == null
? false
: this.middle.removeNGC(key.substring(1), purge);
}
} else if (c.compareTo(this.character) < 0) {
return left == null ? false : left.removeNGC(key, purge);
} else {
return right == null ? false : right.removeNGC(key, purge);
}
}
Enter fullscreen mode Exit fullscreen mode
Moreover, the point is that if you expect the deleted keys to be added again shortly after, then clearing up those nodes and re-allocating them becomes a huge waste of resources.
So, how do you know which version you should implement? There is no answer but: study the context and requirements, and run some profiling – let the data suggest you what to do.
Conclusions
If you read it this far, you got an idea of how the core methods for TSTs work.
It’s time to take a break to process all these new information, but stay tuned, I’ll go over prefix search and how to use it for cool stuff like autocomplete or spell check in the next posts.
(String) Prefix Trees (5 Part Series)
1 Implementing Tries in Java
2 Ternary Search Trees
3 Ternary Search Tree: Core Methods (Java Implementation)
4 Prefix Search with Ternary Search Trees (Java Implementation)
5 Java Profiling: comparing BSTs, tries and TSTs
原文链接:Ternary Search Tree: Core Methods (Java Implementation)

























暂无评论内容