What is Quicksort

Quicksort is a popular and common sorting algorithm that known to be really efficient. It createn 1959, and published in 1961 by Tony Hoare (He’s known for Null reference, Processes and Structured Programming etc. too).

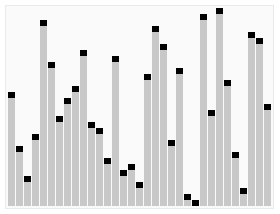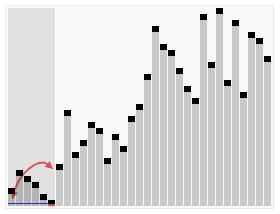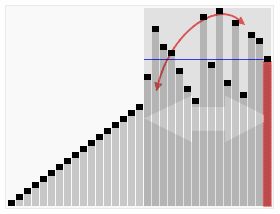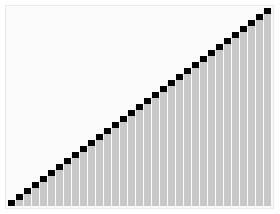
Then, let’s get into algorithm. If we need to visualize the algorithm, we can visualize it like this:

How algorithm works:

• Check if list is empty or vice versa
  If the list is one element return the element,
  else, continue to the function.

• Select a pivot
  Pivot is generally being the first element of list.
  But pivot can be any element of list too.
  For example:

[b, a, d, e, c], Our pivot is b

• Filter the smaller/bigger numbers than pivot (a) Basically, you should iterate on elements of list, and get the bigger numbers than pivot (a). Then, you should do the same thing for the smaller numbers too. For example:

bigger = Filter numbers in [b, a, d, e, c] bigger than a
smaller = Filter numbers in [b, a, d, e, c] smaller than or equal to a

• Sort the filtered bigger and smaller numbers and concenate them Now, we will sort (using same algorithm the bigger and smaller numbers to get order in them and concenate it with the pivot (a)

quicksort(smaller) + [a] + quicksort(bigger)

Then we finished our algorithm! Now, let’s implement it in Python & OCaml.

I tried to comment Python alot to beginners understand the code.

def quicksort(array):
  if not array: # If list is empty     return []
  pivot = array[0] # Pivot is the first element of list   smaller = [n for n in array if n < pivot] # Filter the smaller numbers   bigger = [n for n in array if n > pivot] # Filter the bigger numbers   return quicksort(smaller) + [pivot] + quicksort(bigger) # Concenate sorted smaller and sorted bigger with pivot 

Now, let’s implement it in OCaml!

let rec quicksort list =
    match list with
    | [] -> []
    | pivot :: _ ->
      let smaller = List.filter (fun n -> n < pivot) list in
      let bigger = List.filter (fun n -> n > pivot) list in
      quicksort(smaller) @ [pivot] @ quicksort(bigger)

Let’s try to run it in repl

# quicksort [5, 1, 9, 4, 6, 7, 3];;
- : (int * int * int * int * int * int * int) list = [(5, 1, 9, 4, 6, 7, 3)]

It works! (After 18 tries)

And finally, the performance of Quicksort is:

• Worst performance: O(n2)
• Average performance: O(n log n)
• Best performance: O(n log n)

The average and best performance is same.

If we need to visualize the sorted list:

(Special thanks to Learn you a Haskell for great good! for photo. It has really good Haskell chapters!)

In the next posts, i’ll share the Quickselect algorithm developed by same person developed Quicksort (Tony Hoare)! Goodbye!

原文链接：What is Quicksort